Mediation with svyset Data
Current versions of Stata support svy: sem and
estat teffects without complaint. There is
no longer a need to use gsem and manual
calculation. However, this document may still be useful as either a
guide to using estat teffects or manually calculating them
if you need to use gsem for another reason.
Mediation models in Stata are fit with the sem command.
sem does not support svyset data, so instead
you use gsem (e.g. svy: gsem ...).
However, gsem does not support estat teffects
which calculates direct, indirect and total effects.
This document shows how to manually calculate these effects using
nlcom.
Note that this is a case where all variables are continuous and all
models are linear - we are only using gsem for it’s support
of svy:, not it’s support of GLMs. Indirect effects are a
more complicated topic in those models which we do not address here.
Additionally, we’ll trust Stata to compute standard errors rather than
getting into any sticky issues of bootstrapping.
Standard Mediation
First, let’s estimate the direct, indirect and total effects without the use of the survey design to show equivalence.
. webuse gsem_multmed (Fictional job-performance data)
The model we’ll be fitting is
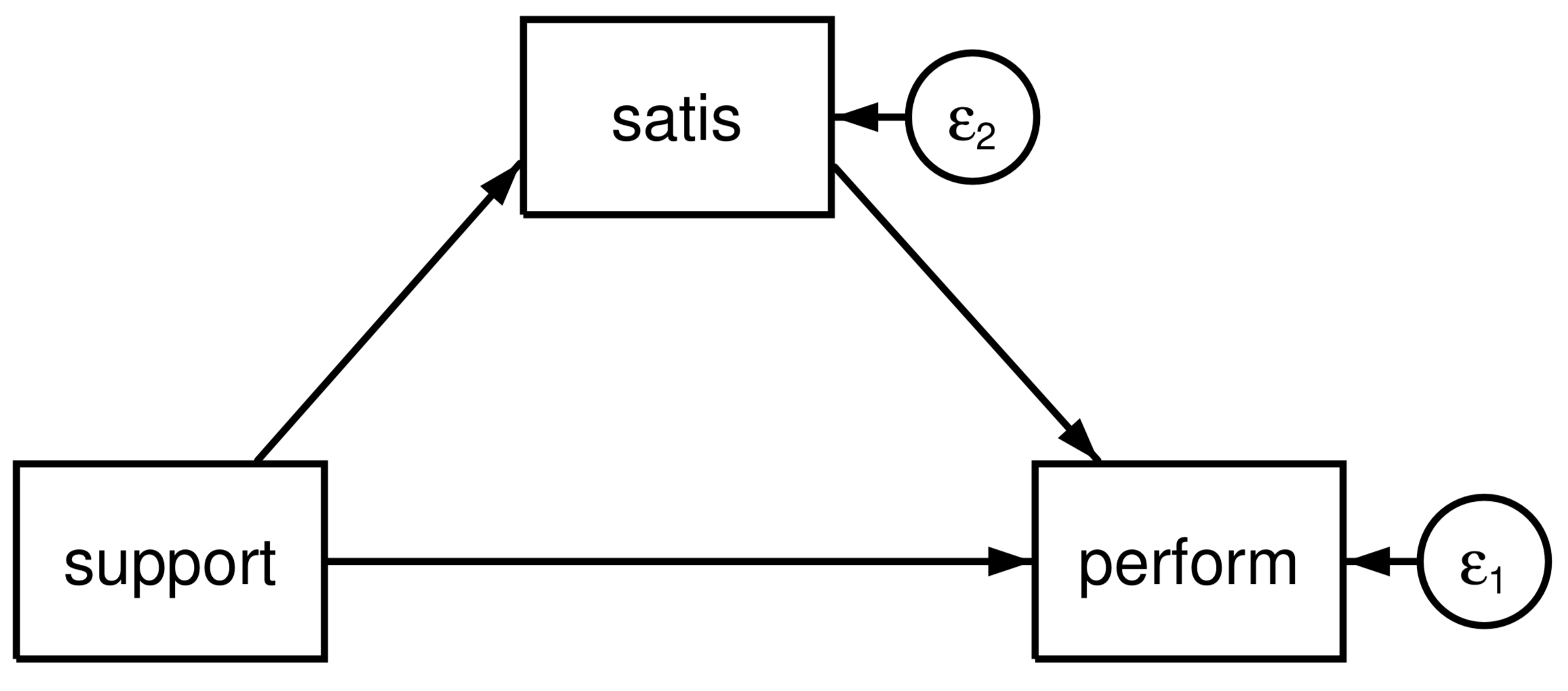
Here, “satis” is a potential mediator between “support” and “perform”. The direct effect is the arrow between “support” and “perform”, the indirect effect is the arrows from “support” to “perform” which passes through “satis”, and the total effect is the sum of the direct and indirect effects.
. sem (perform <- satis support) (satis <- support)
Endogenous variables
Observed: perform satis
Exogenous variables
Observed: support
Fitting target model:
Iteration 0: Log likelihood = -3779.9224
Iteration 1: Log likelihood = -3779.9224
Structural equation model Number of obs = 1,500
Estimation method: ml
Log likelihood = -3779.9224
------------------------------------------------------------------------------
| OIM
| Coefficient std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
Structural |
perform |
satis | .8984401 .0251903 35.67 0.000 .849068 .9478123
support | .6161077 .0303143 20.32 0.000 .5566927 .6755227
_cons | 4.981054 .0150589 330.77 0.000 4.951539 5.010569
-----------+----------------------------------------------------------------
satis |
support | .2288945 .0305047 7.50 0.000 .1691064 .2886826
_cons | .019262 .0154273 1.25 0.212 -.0109749 .0494989
-------------+----------------------------------------------------------------
var(e.perf~m)| .3397087 .0124044 .3162461 .364912
var(e.satis)| .3569007 .0130322 .3322507 .3833795
------------------------------------------------------------------------------
LR test of model vs. saturated: chi2(0) = 0.00 Prob > chi2 = .
The direct, indirect and total effects can be estimated via
estat teffects.
. estat teffects
Direct effects
------------------------------------------------------------------------------
| OIM
| Coefficient std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
Structural |
perform |
satis | .8984401 .0251903 35.67 0.000 .849068 .9478123
support | .6161077 .0303143 20.32 0.000 .5566927 .6755227
-----------+----------------------------------------------------------------
satis |
support | .2288945 .0305047 7.50 0.000 .1691064 .2886826
------------------------------------------------------------------------------
Indirect effects
------------------------------------------------------------------------------
| OIM
| Coefficient std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
Structural |
perform |
satis | 0 (no path)
support | .205648 .0280066 7.34 0.000 .150756 .26054
-----------+----------------------------------------------------------------
satis |
support | 0 (no path)
------------------------------------------------------------------------------
Total effects
------------------------------------------------------------------------------
| OIM
| Coefficient std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
Structural |
perform |
satis | .8984401 .0251903 35.67 0.000 .849068 .9478123
support | .8217557 .0404579 20.31 0.000 .7424597 .9010516
-----------+----------------------------------------------------------------
satis |
support | .2288945 .0305047 7.50 0.000 .1691064 .2886826
------------------------------------------------------------------------------
Let’s calculate them manually. First we’ll re-display the SEM results
with the coeflegend to obtain the names to access the
coefficients.
. sem, coeflegend
Structural equation model Number of obs = 1,500
Estimation method: ml
Log likelihood = -3779.9224
------------------------------------------------------------------------------
| Coefficient Legend
-------------+----------------------------------------------------------------
Structural |
perform |
satis | .8984401 _b[perform:satis]
support | .6161077 _b[perform:support]
_cons | 4.981054 _b[perform:_cons]
-----------+----------------------------------------------------------------
satis |
support | .2288945 _b[satis:support]
_cons | .019262 _b[satis:_cons]
-------------+----------------------------------------------------------------
var(e.perf~m)| .3397087 _b[/var(e.perform)]
var(e.satis)| .3569007 _b[/var(e.satis)]
------------------------------------------------------------------------------
LR test of model vs. saturated: chi2(0) = 0.00 Prob > chi2 = .
The main effects are directly from the model, but for completeness let’s obtain it.
. estat teffects, noindirect nototal
Direct effects
------------------------------------------------------------------------------
| OIM
| Coefficient std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
Structural |
perform |
satis | .8984401 .0251903 35.67 0.000 .849068 .9478123
support | .6161077 .0303143 20.32 0.000 .5566927 .6755227
-----------+----------------------------------------------------------------
satis |
support | .2288945 .0305047 7.50 0.000 .1691064 .2886826
------------------------------------------------------------------------------
. nlcom _b[perform:support]
_nl_1: _b[perform:support]
------------------------------------------------------------------------------
| Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
_nl_1 | .6161077 .0303143 20.32 0.000 .5566927 .6755227
------------------------------------------------------------------------------
For the indirect effect, we’ll simply multiply the path from “support” to “satis” and from “satis” to “perform”.
. estat teffects, nodirect nototal
Indirect effects
------------------------------------------------------------------------------
| OIM
| Coefficient std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
Structural |
perform |
satis | 0 (no path)
support | .205648 .0280066 7.34 0.000 .150756 .26054
-----------+----------------------------------------------------------------
satis |
support | 0 (no path)
------------------------------------------------------------------------------
. nlcom _b[perform:satis]*_b[satis:support]
_nl_1: _b[perform:satis]*_b[satis:support]
------------------------------------------------------------------------------
| Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
_nl_1 | .205648 .0280066 7.34 0.000 .150756 .26054
------------------------------------------------------------------------------
Finally, we can sum those for the direct effect.
. estat teffects, nodirect noindirect
Total effects
------------------------------------------------------------------------------
| OIM
| Coefficient std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
Structural |
perform |
satis | .8984401 .0251903 35.67 0.000 .849068 .9478123
support | .8217557 .0404579 20.31 0.000 .7424597 .9010516
-----------+----------------------------------------------------------------
satis |
support | .2288945 .0305047 7.50 0.000 .1691064 .2886826
------------------------------------------------------------------------------
. nlcom _b[perform:satis]*_b[satis:support] + _b[perform:support]
_nl_1: _b[perform:satis]*_b[satis:support] + _b[perform:support]
------------------------------------------------------------------------------
| Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
_nl_1 | .8217557 .0404579 20.31 0.000 .7424597 .9010516
------------------------------------------------------------------------------
With Survey Data
We’ll reproduce the above results with survey set data. The actually
svyset here is nonsense, this test data is not actual survey
data.
. svyset branch [pweight = perform]
Sampling weights: perform
VCE: linearized
Single unit: missing
Strata 1:
Sampling unit 1: branch
FPC 1:
Finally, all three effects can be calculated via the
same nlcom commands.
. svy: gsem (perform <- satis support) (satis <- support)
(running gsem on estimation sample)
Survey: Generalized structural equation model
Number of strata = 1 Number of obs = 1,500
Number of PSUs = 75 Population size = 7,507.976
Design df = 74
Response: perform
Family: Gaussian
Link: Identity
Response: satis
Family: Gaussian
Link: Identity
------------------------------------------------------------------------------
| Linearized
| Coefficient std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
perform |
satis | .8768337 .0478296 18.33 0.000 .781531 .9721363
support | .6105411 .0276199 22.11 0.000 .5555072 .665575
_cons | 5.051254 .0414936 121.74 0.000 4.968576 5.133932
-------------+----------------------------------------------------------------
satis |
support | .212986 .0261195 8.15 0.000 .1609418 .2650301
_cons | .0841272 .0583215 1.44 0.153 -.032081 .2003353
-------------+----------------------------------------------------------------
var(e.perf~m)| .3284831 .0241911 .2836511 .3804009
var(e.satis)| .3570689 .0353162 .2931998 .4348508
------------------------------------------------------------------------------