Visualizing Collinearity

While there are many resources out there to describe the issues arising with multicollinearity in independent variables, there’s a visualization for the problem that I came across in a book once and haven’t found replicated online. This replicates the visualization.

Set-up

Let Y be a response and X₁ and X₂ be the predictors, such that

Y_{i} = β_{0} + β_{1} X_{1 i} + β_{2} X_{2 i} + ε_{i}

for individual i.

For simplicity, let’s say that

β_{0} = 0, β_{1} = 1, β_{2} = 1 .

I carry out a simulation by generating 1,000 data-sets with a specific correlation between predictors and obtain their coefficients.

reps <- 1000
        n <- 100
        save <- matrix(nrow = reps, ncol = 3)

        for (i in 1:reps) {
        x1 <- rnorm(n)
          x2 <- rnorm(n)
          y <- x1 + x2 + rnorm(n)

          mod <- lm(y ~ x1 + x2)
          save[i, ] <- c(coef(mod)[-1], cor(x1, x2))
          }

The line x2 <- rnorm(n) gets replaced with x2 <- x1 + rnorm(n, sd = _), where the _ is replaced with difference values to induce more correlation between x1 and x2.

Simulation Results

Low Moderate High Extreme

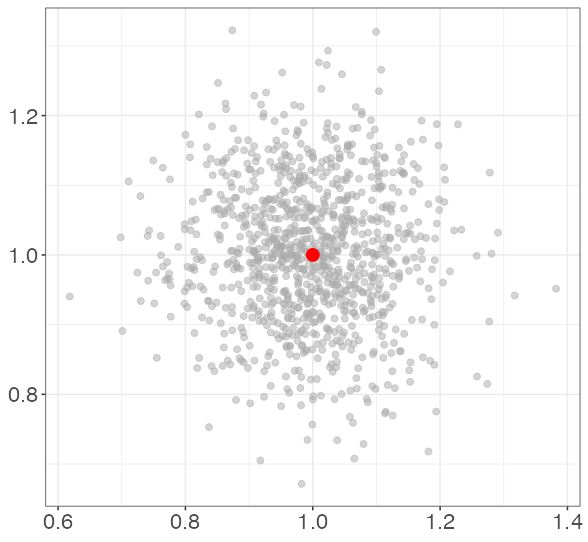
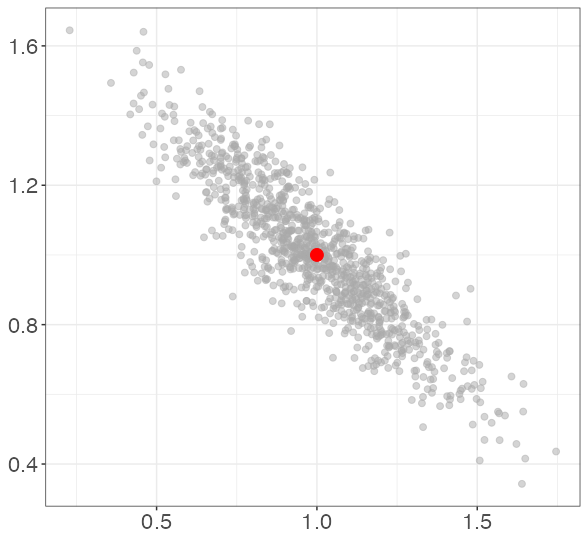
Each point represents the estimated coefficients for a single simulated data set. The red dot represents the data-generating coefficients (1, 1). Note that bias is not a concern; the true coefficients are on average for each level of collinearity.

In this simulation, the average correlation between X₁ and X₂ is 0.002. 0.554. 0.894. 0.995.

With low correlation, we see no relationship between the estimated coefficients. While we are starting to see a correlation between the coefficients, it is not that strong yet. With correlation around .9, we are seeing very strong collinearity: if

{\hat{X}}_{1}

is low, then we would expect

{\hat{X}}_{2}

to be high. This relationship is incredibly strong.

Why is this a problem?

So this simulation shows that at correlations around .9 or higher between X₁ and X₂, there is negative correlation between ${\hat{X}}_{1}$ and ${\hat{X}}_{2}$ . Why is this a problem?

Consider the “extremely high correlation” results. With such high correlation, we have that $X_{1} \approx X_{2}$ We can use this approximate equality to rewrite the model:

\begin{aligned} Y_{i} & = β_{0} + β_{1} X_{1 i} + β_{2} X_{2 i} + ε_{i} \\ \approx β_{0} + (β_{1} + β_{2}) X_{1 i} + ε_{i} \\ \approx β_{0} + (β_{1} + β_{2}) X_{2 i} + ε_{i} \end{aligned}

In other words, the model has that $β_{1} + β_{2} = 2$ (since we assumed above that both coefficients have values of 1). So while all of those models would have the same predictive power for Y, they would have drastically different interpretations. For example, we could obtain ${\hat{X}}_{1} = - 1$ and ${\hat{X}}_{2} = 3$ , which not only over-emphasizes the relationship betwen X₂ and Y, but suggests a inverse relationship between X₁ and Y!